Jährliche Trigonometrische Parallaxe von Sternen
Entfernungsbestimmung
mit der Trigonometrische Parallaxe
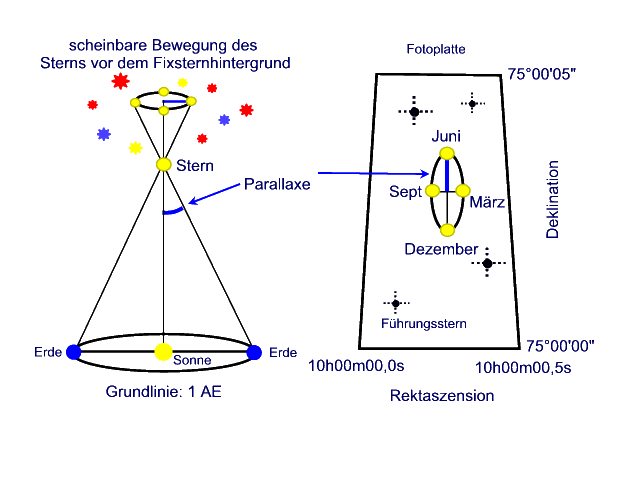
Annahme: Stern und Sonne mögen ruhen. Visiert man den Stern von der Erde an, so beschreibt der Stern im Laufe eines Jahres eine Ellipse an der Sphäre. Diese Verschiebung bezeichnet man als Parallaxe (Hin- und Herbewegen). Je nach Lage des Sterns ergibt sich ein Kreis, eine Ellipse oder eine Strecke. Friedrich Wilhelm Bessel hat die ersten, sehr guten Fixsternparallaxen im 19. Jahrhundert bestimmt. Die Parallaxe kann aus dem Winkeldurchmesser des Kreises, der Ellipse bzw. der Strecke durch mehrere Fotographien im Laufe eines Jahres bestimmt werden. Die bekannten Koordinaten weit entfernter Sterne normieren die Aufnahme.
Definition der
Entfernungseinheit Parsec (Parallaxensekunde, pc)
1
Parsec = 1 pc = Entfernung, aus der der Erdbahnradius
unter einem Winkel von 1 Bogensekunde erscheint
Definition
der Jährlichen trigonometrischen Parallaxe
Der Winkel p, unter dem vom Stern aus der
Erdbahnradius erscheint, heißt jährliche
trigonometrische Parallaxe
Im
Dreieck Stern – Sonne – Erde gilt: sin p = AE/r. Für sehr kleine
Parallaxenwinkel gilt:
sin p = p ( p im Bogenmaß)
| Es folgt: |
|
oder |
|
Für
die Entfernungseinheit ergibt sich daher:
| 1 pc = |
|
=206246,8 AE=3,0857.1016 m = 3,26 Lj |
Definition Lichtjahr
1 Lichtjahr = 1 Lj = Entfernung, die das Licht im Vakuum in einem Jahr zurücklegt.
Somit verfügen wir über eine Möglichkeit, die
Entfernung eines Sterns zu bestimmen:
|
|
= |
|
mit 1“ und p
im Gradmaß |
Bei messbaren Parallaxen von 0,01“ erhält man
einen maximalen Abstand von 100 pc oder etwa 300 Lichtjahren. Zur Zeit von
Kopernikus und Kepler hätte der Nachweis der Fixsternparallaxe den Beweis für
das heliozentrische Weltbild erbracht. Wegen der damaligen Messgenauigkeit von bestenfalls
2´ ergibt sich ein Abstand von höchstens 0,008 pc. Dies reicht nicht einmal bis zum nächsten
Fixstern. Erst Friedrich Wilhelm Bessel in Königsberg konnte1838 mit einem von
Fraunhofer entworfenem Fernrohr, dem Heliometer für das Doppelsternsystem 61 Cygni
die
Parallaxe mit 0,31" bestimmen. Diese Beobachtung ist der erste
physikalische Beweis, dass sich die Erde um die Sonne bewegt.
| Name | Rektaszension | Deklination | Parallaxe | pc | LJ |
| Proxima Centauri | 14h30m6 | -62° 42' | 0,762" | 1,31 | 4,28 |
| Sirius A/B | 6h45m1 | -16° 42' | 0,375 | 2,67 | 8,69 |
| 61Cygni A/B | 21h06m6 | +38° 42' | 0,292 | 3,42 | 11,16 |
Die Messung der trigonometrischen Parallaxe ist mit einigen Problemen verbunden:
Eigenbewegung der
Sterne, nur in Ausnahmen feststellbar
Aberration des
Lichtes
Vergleich: Eigenbewegung bei Regen
1725: Bradley:
jährliche
Aberration
wegen der Bewegung der Erde
mit v = 30 km/s
Atmosphärische Refraktion: Lichtbrechung in der Atmosphäre
Eigenbewegung der Sonne
Für
Entfernungen bis 100 Lj ist die Methode der trigonometrischen Parallaxe anwendbar.
Auf diesen Seite findet man eine Auflistung von Sternen im Umkreis von der Sonne:
The Universe within 12.5 Light Years
The Universe within 250 Light Years - The Solar Neighbourhood
The Universe within 5000 Light Years - The Orion Arm
Nun kann man für diese Sterne einige physikalische Werte wie die
Leuchtkraft bestimmen. Unter der Annahme, dass auch für weiter entfernte Sterne
gleiche physikalische Rahmenbedingungen bestehen, kann man basierend auf den
erhaltenen Ergebnissen andere Entfernungsbestimmungsmethoden entwickeln.