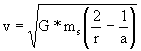Mechanische
Energien eines Planeten
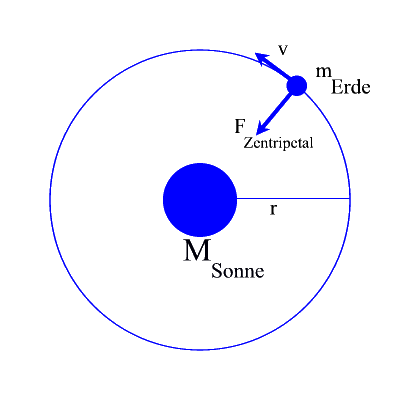
Objekt auf einer Kreisbahn
|
Aus dem Kräfteansatz
FZentripetal = FGravitation mit folgt die Geschwindigkeit, die ein Planet haben muss, um sich auf einer Kreisbahn um die Zentralmasse halten zu können.
Für einen Satelliten, der in Erdnähe die Erde auf
einer Kreisbahn umrundet, beträgt dieser Wert 7,8 km/s. Die Erde bewegt sich um
die Sonne mit 30 km/s. |
 |
Auf der Kreisbahn sind die kinetische Energie und
die potentielle Energie jede für sich konstant.
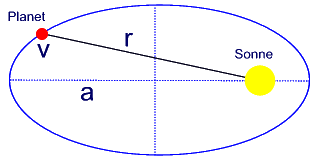
Objekt auf einer Ellipsenbahn
Auf
einer Ellipsenbahn dagegen wandeln sich die beiden Energieformen ständig
ineinander um. Die Summe aus kinetischer und potentieller Energie ist aber wegen
des Energieerhaltungsatzes konstant. Aus dieser Idee und dem 2. Kepler-Gesetz
kann eine Formel für die Bahngeschwindigkeit eines Planeten auf einer Ellipse
abgeleitet werden.
|
Bahngeschwindigkeit eines Körpers auf einer
Ellipse mit großer Halbachse a im Abstand
r vom Zentralkörper |
 |
Flucht eines Objekts aus dem Schwerefeld eines
Zentralkörpers
Um im Schwerefeld eines Planeten oder der Sonne, allgemein einer Masse, einen Körper in eine größere Entfernung r zu bringen, muss "Hubarbeit" verrichtet werden. Da die Gravitation aber vom Abstand abhängt, also nicht konstant ist, ist die Berechnung der Hubarbeit etwas aufwändiger.
Um einen Körper (Satellit usw.) m vom momentanen Abstand r zu einer Zentralmasse M bis ins Unendliche zu transportieren, muss Arbeit verrichtet werden. Diese Arbeit kann z.B. durch eine anfangs vorhandene kinetische Energie aufgebracht werden.
![]()
mit dem Erdradius r und nach Umformen
![]()
Beipiel: eine Rakete soll von der Erde mit einer
Mindestgeschwindigkeit starten und das Gravitationsfeld der Erde völlig
verlassen.
Für die Erde ergibt sich die 2. Fluchtgeschwindigkeit
11,2 km/s.
Die drei Fälle Kreisbahn, Ellipse und Flucht ins
Unendliche sind in der Geschwindigkeitsformel für die Ellipse enthalten.